Operator learning is a transformative approach in scientific computing. It focuses on developing models that map functions to other functions, an essential aspect of solving partial differential equations (PDEs). Unlike traditional neural network tasks, these mappings operate in infinite-dimensional spaces, making them particularly suitable for scientific domains where real-world problems inherently exist in expansive mathematical frameworks. This methodology is pivotal in applications like weather forecasting, fluid dynamics, and structural analysis, where the need for efficient and accurate computations often outpaces the capabilities of current methods.
Scientific computing has long faced a fundamental challenge in solving PDEs. Traditional numerical methods rely on discretization, breaking down continuous problems into finite segments to facilitate computation. However, the accuracy of these solutions depends heavily on the resolution of the computational meshes. High-resolution meshes offer precise results but come at the cost of substantial computational power and time, often rendering them impractical for large-scale simulations or parameter sweeps. Moreover, the lack of generalization across different discretizations further hampers the applicability of these methods. The need for a robust, resolution-agnostic solution that can handle diverse and complex data has remained an unmet challenge in the field.
In the existing toolkit for PDEs, machine learning models have been explored as an alternative to traditional numerical techniques. These models, including feed-forward neural networks, approximate solutions directly from input parameters, bypassing some computational overhead. While these methods improve computational speed, they are limited by their reliance on fixed discretization frameworks, which restricts their adaptability to new data resolutions. Techniques such as Fast Fourier Transforms (FFT) have also contributed by enabling efficient computation for problems defined over regular grids. However, these methods fall short in flexibility and scalability when applied to function spaces, exposing a critical limitation that researchers sought to address.
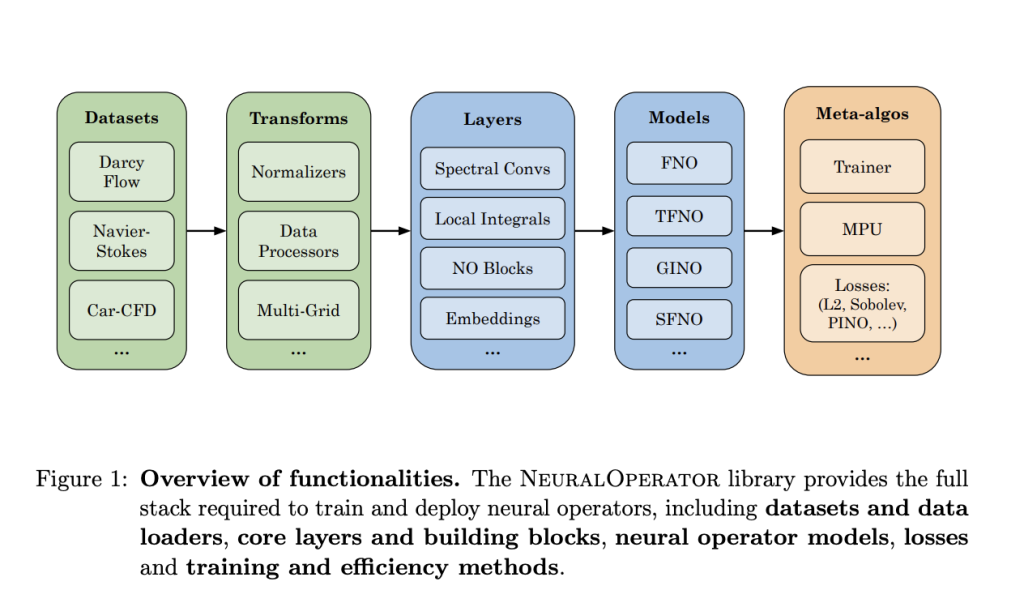
Researchers from NVIDIA and Caltech have introduced NeuralOperator, a new Python library designed to address these shortcomings. NeuralOperator redefines operator learning by enabling the mapping of function spaces while ensuring flexibility across discretizations. It is built on PyTorch and provides an accessible platform for training and deploying neural operator models, allowing users to solve PDE-based problems without being constrained by discretization. This tool is modular and robust, catering to newcomers and advanced scientific machine-learning practitioners. The library’s design principles emphasize resolution-agnosticity, ensuring that models trained on one resolution can seamlessly adapt to others, a significant step forward from traditional neural networks.
The technical underpinnings of NeuralOperator are rooted in its use of integral transforms as a core mechanism. These transforms allow the mapping of functions across diverse discretizations, leveraging techniques such as spectral convolution for computational efficiency. The Fourier Neural Operator (FNO) employs these spectral convolution layers and introduces tensor decompositions to reduce memory usage while enhancing performance. Tensorized Fourier Neural Operators (TFNOs) further optimize this process through architectural improvements. Geometry-informed Neural Operators (GINOs) also incorporate geometric data, enabling models to adapt to varied domains, such as irregular grids. NeuralOperator also supports super-resolution tasks, where input and output data operate at different resolutions, expanding its versatility in scientific applications.
Tests conducted on benchmark datasets, including Darcy Flow and Navier-Stokes equations, reveal a marked improvement over traditional methods. For example, FNO models achieved less than 2% error rates in predicting fluid dynamics over high-resolution grids. The library also supports distributed training, enabling large-scale operator learning across computational clusters. Features like mixed-precision training further enhance its utility by reducing memory requirements, allowing for the efficient handling of large datasets and complex problems.
Key takeaways from the research highlight the potential of NeuralOperator in scientific computing:
- NeuralOperator models generalize seamlessly across different discretizations, ensuring flexibility and adaptability in various applications.
- Techniques like tensor decomposition and mixed-precision training reduce resource consumption while maintaining accuracy.
- The library’s components are suitable for beginners and advanced users, enabling rapid experimentation and integration into existing workflows.
- By supporting datasets for equations like Darcy Flow and Navier-Stokes, NeuralOperator applies to a wide range of domains.
- FNOs, TFNOs, and GINOs incorporate cutting-edge techniques, enhancing performance and scalability.
In conclusion, the findings from this research offer a robust solution to long-standing challenges in scientific computing. NeuralOperator’s ability to handle infinite-dimensional function mappings, its resolution-agnostic properties, and its efficient computation make it an indispensable tool for solving PDEs. Also, its modularity and user-centric design lower the entry barrier for new users while providing advanced features for experienced researchers. As a scalable and adaptable framework, NeuralOperator is poised to advance the field of scientific machine learning significantly.
Check out the Paper 1, Paper 2, and GitHub Page. All credit for this research goes to the researchers of this project. Also, don’t forget to follow us on Twitter and join our Telegram Channel and LinkedIn Group. Don’t Forget to join our 60k+ ML SubReddit.
Trending: LG AI Research Releases EXAONE 3.5: Three Open-Source Bilingual Frontier AI-level Models Delivering Unmatched Instruction Following and Long Context Understanding for Global Leadership in Generative AI Excellence….The post NeuralOperator: A New Python Library for Learning Neural Operators in PyTorch appeared first on MarkTechPost.
Source: Read MoreÂ
