Quantum and neuromorphic computing represent phenomenal computational paradigms that promise transformative technological advances. Quantum computing utilizes unique quantum phenomena like entanglement and superposition to develop algorithms that surpass classical computational methods. Neuromorphic computing draws inspiration from biological neural networks to achieve energy-efficient computational strategies. The convergence of these two innovative fields has recently emerged as quantum neuromorphic computing (QNC), a multidisciplinary approach that synthesizes quantum mechanical principles with neural computational dynamics. This emerging field explores the intriguing similarities between neural network behaviors and quantum system dynamics, particularly focusing on developing noise-resilient and scalable algorithms for quantum machine learning applications.
Researchers from the Department of Computing + Mathematical Sciences (CMS), California Institute of Technology (Caltech), Department of Physics, Indian Institute of Technology Kanpur, Uttar Prades, NVIDIA, Department of Physics, and Harvard University present this study on the intricate mechanics of implementing quantum perceptrons (QPs) on Rydberg atom arrays, exploring sophisticated experimental strategies for quantum computation. The study focuses on utilizing specific atomic arrangements to exploit Van der Waals potentials and flip-flop Hamiltonians in single-species arrays while also proposing dual-species arrays to minimize cross-talk between input qubits. Beyond implementation techniques, the research demonstrates the robust classification capabilities of QPs by successfully distinguishing between quantum phases and performing entanglement classification under diverse noise conditions. A significant advancement involves extending the QP model to incorporate two output qubits, enabling more scalable and efficient multi-class classification and paving the way for more complex neural network architectures in quantum computing.
What is a Quantum Perceptron?
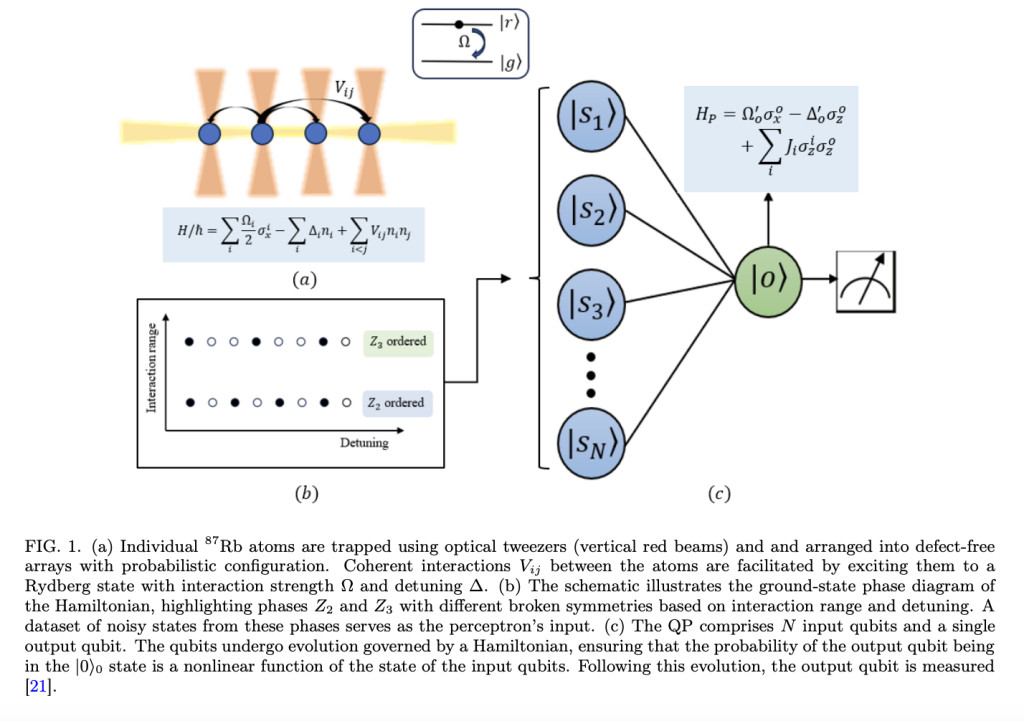
A quantum perceptron represents a quantum-mechanical evolution of the classical perceptron, a simplified model of biological neurons fundamental to machine learning and artificial neural networks for classification tasks. Formally, a QP consists of N+1 qubits, with N input qubits and a single output qubit. Each input qubit mirrors the input neurons in classical perceptrons, interacting with the output qubit through quantum Hamiltonian dynamics. The entire quantum system exists within a product Hilbert space, with each qubit occupying its individual Hilbert space defined by basis vectors |0⟩ and |1⟩. This quantum architectural design enables sophisticated interactions and computational capabilities that transcend traditional neural network models, offering unprecedented potential for complex computational tasks.
Learning with Quantum Perceptrons
Quantum perceptrons gain remarkable computational capabilities through the introduction of rotations on input and output qubits, enabling universal quantum computation. By incorporating a universal gate set, specifically the Clifford+T set, QPs demonstrate computational complexity that significantly surpasses classical perceptron models. Researchers have transformed QPs into variational circuits, effectively transitioning them from mere quantum circuit components to foundational elements of an innovative quantum machine learning architecture. In this approach, single-qubit rotations are treated as unitaries, while Hamiltonian function evolutions serve as entangling unitaries. This sophisticated design allows QPs to transcend traditional computational boundaries, offering a powerful framework for advanced learning tasks that utilize quantum mechanical principles.
What are Rydberg Arrays?
Rydberg atoms are characterized by two primary electronic states: the ground state |g⟩ and the excited Rydberg state |r⟩, which can be accessed through a two-photon optical transition. These atoms are strategically positioned in predetermined spatial configurations, initially existing in a well-defined ground state. Laser light facilitates time evolution by coupling atoms to their Rydberg states along the array’s axis. State readout occurs through reactivating traps and imaging ground-state atoms via atomic fluorescence, with Rydberg atoms being simultaneously expelled. A distinctive feature of Rydberg atoms is their strong, repulsive van der Waals interactions, which scale with the inverse sixth power of interatomic distance. This interaction mechanism provides a unique platform for exploring complex quantum computational dynamics.
The researchers evaluated the QP’s accuracy across three primary classification challenges: distinguishing states within Z2, Z3, and Z4 phases, which emerge from complex interactions between coherent coupling and interatomic forces. These phases represent unique spatial ordering and symmetry-breaking configurations characterized by specific quantum state arrangements. To rigorously test the QP’s performance, the study introduced a controlled 30% probability amplitude error margin, simulating realistic quantum state determination challenges.
Multi-layer perceptrons (MLPs) represent sophisticated artificial neural networks composed of multiple neuron layers. To advance quantum perceptron architectures, researchers extended the existing model to incorporate two output qubits, enabling more complex multi-class classification capabilities. This architectural enhancement allows each output qubit to independently interact with all input qubits, significantly expanding the computational potential of quantum neural networks. The two-output qubit design enables more nuanced and comprehensive quantum information processing, offering a pathway to deeper and more expressive quantum neural network architectures. By modifying the underlying Hamiltonian equations, the researchers demonstrated a scalable approach to developing more advanced quantum computational models.
The study comprehensively explores quantum perceptrons implemented through Rydberg atom arrays, demonstrating their remarkable potential in quantum machine learning. By mapping Rydberg Hamiltonians onto perceptron dynamics, the researchers successfully showcased QPs’ effectiveness in classifying quantum phases with different broken symmetries and performing entanglement classification under varying noise conditions. Two primary experimental strategies were investigated: single-species arrays utilizing Van der Waals and flip-flop Hamiltonians and dual-species arrays employing different atomic species for input and output qubit encoding. The research also established the approximation capabilities of QPs, revealing their ability to approximate continuous functions with a logarithmically scaling computational complexity.
Check out the Paper. All credit for this research goes to the researchers of this project. Also, don’t forget to follow us on Twitter and join our Telegram Channel and LinkedIn Group. If you like our work, you will love our newsletter.. Don’t Forget to join our 55k+ ML SubReddit.
The post Quantum Neuromorphic Computing: Implementing Scalable Quantum Perceptrons appeared first on MarkTechPost.
Source: Read MoreÂ

 ‘
‘