Large Language Models (LLMs) have demonstrated remarkable in-context learning (ICL) capabilities, where they can learn tasks from demonstrations without requiring additional training. A critical challenge in this field is understanding and predicting the relationship between the number of demonstrations provided and the model’s performance improvement, known as the ICL curve. This relationship needs to be better understood despite its significant implications for various applications. Accurate prediction of ICL curves holds crucial importance for determining optimal demonstration quantities, anticipating potential alignment failures in many-shot scenarios, and assessing the fine-tuning required to control undesired behaviours. The ability to model these learning curves effectively would enhance decision-making in deployment strategies and help mitigate potential risks associated with LLM implementations.
Various research approaches have attempted to decode the underlying mechanisms of in-context learning in Large Language Models, with divergent theories emerging. Some studies suggest LMs trained on synthetic data behave like Bayesian learners, while others propose they follow gradient descent patterns, and some indicate the learning algorithm varies based on task complexity, model scale, and training progress. Power laws have emerged as a predominant framework for modeling LM behavior, including ICL curves across different settings. However, existing research has notable limitations. No previous work has directly modeled the ICL curve based on fundamental learning algorithm assumptions. Also, post-training modifications have proven largely ineffective, with studies revealing that such changes are often superficial and easily circumvented, particularly concerning since ICL can reinstate behaviors that were supposedly suppressed through fine-tuning.
Researchers propose a that introduces Bayesian laws to model and predict in-context learning curves across different language model scenarios. The study evaluates these laws using both synthetic data experiments with GPT-2 models and real-world testing on standard benchmarks. The approach extends beyond simple curve fitting, providing interpretable parameters that capture the prior task distribution, ICL efficiency, and example probabilities across different tasks. The research methodology encompasses two main experimental phases: first comparing the Bayesian laws’ performance against existing power law models in curve prediction, and second, analyzing how post-training modifications affect ICL behavior in both favored and disfavored tasks. The study culminates in comprehensive testing across large-scale models ranging from 1B to 405B parameters, including evaluation of capabilities, safety benchmarks, and a robust many-shot jailbreaking dataset.
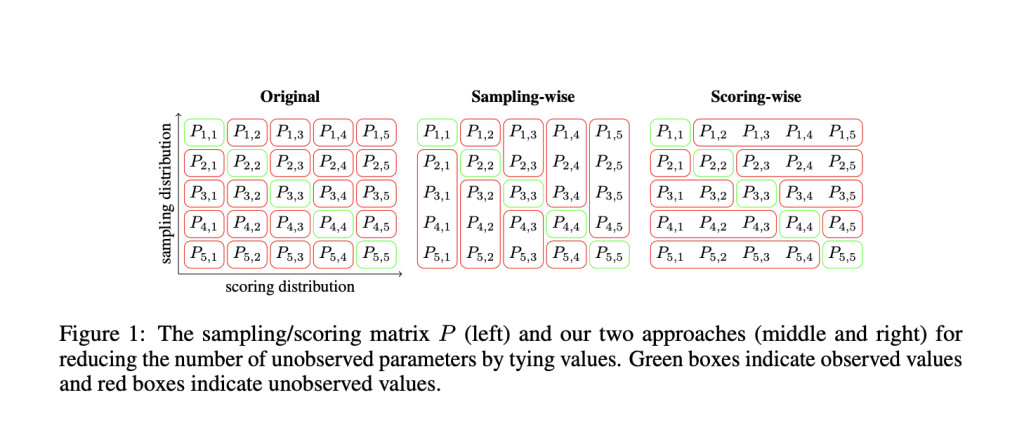
The architecture of the Bayesian scaling laws for ICL is built upon fundamental assumptions about how language models process and learn from in-context examples. The framework begins by treating ICL as a Bayesian learning process, applying Bayes’ theorem iteratively to model how each new in-context example updates the task prior. A key innovation in the architecture is the introduction of parameter reduction techniques to prevent overfitting. This includes two distinct approaches to parameter tying, sampling-wise and scoring-wise, which help maintain model efficiency while scaling linearly with the number of distributions. The architecture incorporates an ICL efficiency coefficient ‘K’ that accounts for the token-by-token processing nature of LLMs and variations in example informativeness, effectively modulating the strength of Bayesian updates based on example length and complexity.
The experimental results demonstrate superior performance of the Bayesian scaling laws compared to existing approaches. In interpolation tests, the original Bayesian scaling law achieved significantly lower Normalized Root Mean Square Error (NRMSE) across model scales and trajectory lengths, only matched by a strong logistic baseline. The scoring-wise Bayesian law particularly excelled in extrapolation tasks, showing the best performance when predicting the remaining 90% of ICL curves using only the first 10% of data points. Beyond numerical superiority, the Bayesian laws offer interpretable parameters that provide meaningful insights into model behavior. The results reveal that prior distributions align with uniform pretraining distributions, and ICL efficiency correlates positively with both model depth and example length, indicating that larger models achieve faster in-context learning, especially with more informative examples.
Comparing Llama 3.1 8B Base and Instruct versions revealed crucial insights about the effectiveness of instruction-tuning. Results show that while instruction-tuning successfully reduces the prior probability of unsafe behaviors across various evaluation metrics (including harmbench and persona evaluations), it fails to prevent many-shot jailbreaking effectively. The Bayesian scaling law demonstrates that posterior probabilities are eventually saturated, regardless of the reduced prior probabilities achieved through instruction-tuning. This suggests that instruction-tuning primarily modifies task priors rather than fundamentally altering the model’s underlying task knowledge, possibly due to the relatively limited computational resources allocated to instruction-tuning compared to pretraining.
The research successfully bridges two fundamental questions about in-context learning by developing and validating Bayesian scaling laws. These laws demonstrate remarkable effectiveness in modeling ICL behavior across both small-scale LMs trained on synthetic data and large-scale models trained on natural language. The key contribution lies in the interpretability of the Bayesian formulation, which provides clear insights into priors, learning efficiency, and task-conditional probabilities. This framework has proven valuable for understanding scale-dependent ICL capabilities, analyzing the impact of fine-tuning on knowledge retention, and comparing base models with their instruction-tuned counterparts. The success of this approach suggests that continued investigation of scaling laws could yield further crucial insights into the nature and behavior of in-context learning, paving the way for more effective and controllable language models.
Check out the Paper and GitHub Page. All credit for this research goes to the researchers of this project. Also, don’t forget to follow us on Twitter and join our Telegram Channel and LinkedIn Group. If you like our work, you will love our newsletter.. Don’t Forget to join our 55k+ ML SubReddit.
[Sponsorship Opportunity with us] Promote Your Research/Product/Webinar with 1Million+ Monthly Readers and 500k+ Community Members
The post Predicting and Interpreting In-Context Learning Curves Through Bayesian Scaling Laws appeared first on MarkTechPost.
Source: Read MoreÂ