Mathematical reasoning within artificial intelligence has emerged as a focal area in developing advanced problem-solving capabilities. AI can revolutionize scientific discovery and engineering fields by enabling machines to approach high-stakes logical challenges. However, complex tasks, especially Olympiad-level mathematical reasoning, continue to stretch AI’s limits, demanding advanced search methods to navigate solution spaces effectively. Recent strides have brought some success in reasoning, yet intricate tasks like multi-step mathematical proofs still need to be solved. This need for high-precision, efficient reasoning pathways motivates ongoing research to enhance the accuracy and reliability of AI models in mathematical contexts.
One major challenge is the development of accurate step-by-step solution paths that AI can use for complex problem-solving. Conventional methods often fail to ensure solution accuracy, especially for multi-step, high-difficulty questions. These methods rely on Chain-of-Thought (CoT) processing, where solutions are broken down into smaller steps, theoretically improving accuracy. However, CoT and its variants need help with tasks requiring deep logical consistency across multiple steps, leading to errors and inefficiencies. The inability to optimize solution paths limits the AI’s capacity to solve complex mathematical problems, highlighting the need for more sophisticated approaches.
Several methods, including Monte Carlo Tree Search (MCTS), Tree-of-Thought (ToT), and Breadth-First Search (BFS), have been developed to address these issues. MCTS and ToT, for instance, aim to improve reasoning by allowing iterative path exploration. However, their greedy search mechanisms can trap the AI in locally optimal but globally suboptimal solutions, significantly lowering the accuracy of complex reasoning tasks. While these approaches provide a foundational structure for solution search, they often need help with the vastness of potential solution spaces in high-level mathematics, ultimately constraining their effectiveness.
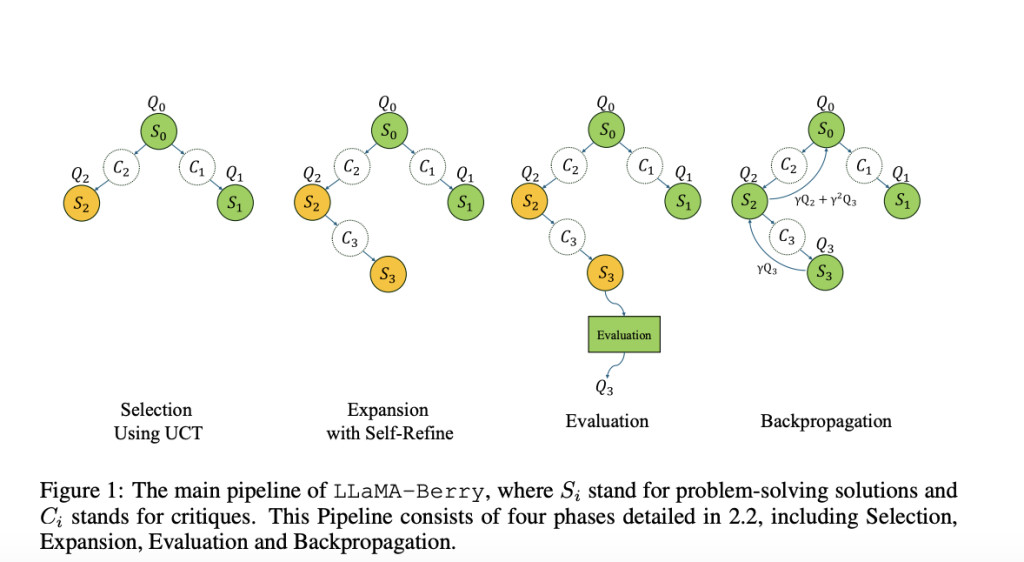
The research team from Fudan University, Shanghai Artificial Intelligence Laboratory, University of California Merced, Hong Kong Polytechnic University, University of New South Wales, Shanghai Jiao Tong University, and Stanford University introduced a pioneering framework called LLaMA-Berry to overcome these challenges. LLaMA-Berry integrates Monte Carlo Tree Search with an innovative Self-Refine (SR) optimization technique that enables efficient exploration and improvement of reasoning paths. The framework utilizes the Pairwise Preference Reward Model (PPRM), which assesses solution paths by comparing them against one another instead of assigning absolute scores. This approach allows for a more dynamic evaluation of solutions, optimizing overall problem-solving performance instead of focusing solely on individual steps.
In LLaMA-Berry, the Self-Refine mechanism treats each solution as a complete state, with MCTS guiding iterative refinements to reach an optimal outcome. This method incorporates a multi-step process involving Selection, Expansion, Evaluation, and Backpropagation phases to balance exploration and exploitation of solution paths. During the Evaluation phase, the PPRM calculates scores based on a comparative ranking. By applying an Enhanced Borda Count (EBC) method, the researchers can aggregate preferences across multiple solutions to identify the most promising paths. PPRM allows for more nuanced decision-making and prevents the AI from overcommitting to any single flawed pathway.
Testing on challenging benchmarks has shown that LLaMA-Berry outperforms existing models in solving Olympiad-level problems. For instance, on the AIME24 benchmark, the framework achieved a performance boost of over 11% compared to prior methods, with an accuracy of 55.1% on Olympiad tasks, marking a significant improvement in handling college-level mathematics. Its success in these tasks indicates that the framework effectively manages complex reasoning without requiring extensive training. This improvement underscores LLaMA-Berry’s capacity to tackle reasoning-heavy tasks more reliably than previous models, showcasing a versatile, scalable solution for complex AI applications.
The most critical finding in LLaMA-Berry’s research is its efficiency in mathematical reasoning tasks due to the integration of Self-Refine and the Pairwise Preference Reward Model. Benchmarks such as GSM8K and MATH showed LLaMA-Berry outperforming open-source competitors, achieving accuracy levels previously only possible with large proprietary models like GPT-4 Turbo. For GSM8K, LLaMA-Berry reached 96.1% with limited simulations, offering high efficiency in rollouts with fewer computational resources. These results illustrate the robustness and scalability of LLaMA-Berry in advanced benchmarks without extensive training.
Key Takeaways from the Research on LLaMA-Berry:
- Benchmark Success: LLaMA-Berry achieved notable accuracy improvements, such as 96.1% on GSM8K and 55.1% on Olympiad-level tasks.
- Comparative Evaluation: The PPRM allows more nuanced evaluation through Enhanced Borda Count, balancing local and global solution preferences.
- Efficient Solution Paths: Self-Refine combined with Monte Carlo Tree Search (MCTS) optimizes reasoning paths, avoiding pitfalls of traditional greedy search methods.
- Resource Efficiency: LLaMA-Berry outperformed open-source models using fewer simulations, achieving 11% to 21% improvements on complex benchmarks.
- Scalability and Adaptability: The framework shows potential to expand beyond mathematical reasoning, offering applicability in multimodal AI tasks across scientific and engineering fields.

In conclusion, LLaMA-Berry represents a substantial advancement in AI, specifically for tackling complex reasoning in mathematics. The framework achieves accuracy and efficiency by leveraging Self-Refine with MCTS and PPRM, surpassing conventional models on Olympiad-level benchmarks. This framework’s scalable approach positions it as a promising tool for high-stakes AI applications, suggesting potential adaptability to other complex reasoning fields, such as physics and engineering.
Check out the Paper and GitHub Page. All credit for this research goes to the researchers of this project. Also, don’t forget to follow us on Twitter and join our Telegram Channel and LinkedIn Group. If you like our work, you will love our newsletter.. Don’t Forget to join our 55k+ ML SubReddit.
[Trending] LLMWare Introduces Model Depot: An Extensive Collection of Small Language Models (SLMs) for Intel PCs
The post LLaMA-Berry: Elevating AI Mathematical Reasoning through a Synergistic Approach of Monte Carlo Tree Search and Enhanced Solution Evaluation Models appeared first on MarkTechPost.
Source: Read MoreÂ