A key question about LLMs is whether they solve reasoning tasks by learning transferable algorithms or simply memorizing training data. This distinction matters: while memorization might handle familiar tasks, true algorithmic understanding allows for broader generalization. Arithmetic reasoning tasks could reveal if LLMs apply learned algorithms, like vertical addition in human learning, or if they rely on memorized patterns from training data. Recent studies identify specific model components linked to arithmetic in LLMs, with some findings suggesting that Fourier features assist in addition tasks. However, the full mechanism underlying generalization versus memorization remains to be determined.
Mechanistic interpretability (MI) seeks to understand language models by dissecting the roles of their components. Techniques such as activation and path patching help link specific behaviors to model parts, while other methods focus on how certain weights influence token responses. Studies also address whether LLMs generalize or simply memorize training data, with insights into how internal activations indicate this balance. For arithmetic reasoning, recent research identifies general structures in arithmetic circuits but needs to include how operand data is processed for accuracy. This study broadens the view, showing how multiple heuristics and feature types combine in LLMs for arithmetic tasks.
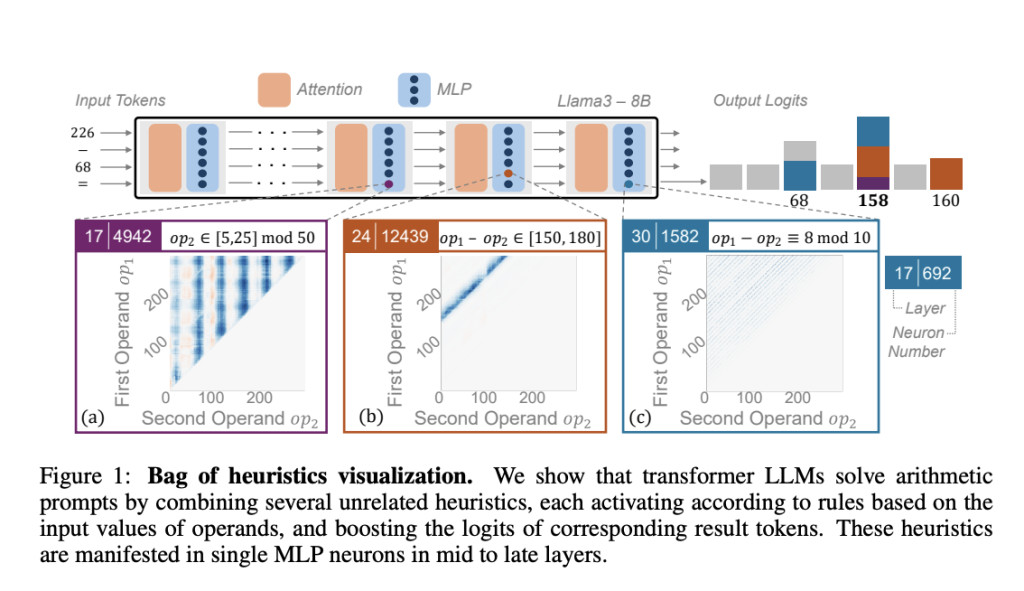
Researchers from Technion and Northeastern University investigated how LLMs handle arithmetic, discovering that instead of using robust algorithms or pure memorization, LLMs apply a “bag of heuristics†approach. Analyzing individual neurons in an arithmetic circuit identified that specific neurons fire according to simple patterns, such as operand ranges, to produce correct answers. This mix of heuristics emerges early in training and persists as the main mechanism for solving arithmetic prompts. The study’s findings provide detailed insights into LLMs’ arithmetic reasoning, showing how these heuristics operate, evolve, and contribute to both capabilities and limitations in reasoning tasks.
In transformer-based language models, a circuit is a subset of model components (MLPs and attention heads) that execute specific tasks, such as arithmetic. Researchers analyzed the arithmetic circuits in four models (Llama3-8B/70B, Pythia-6.9B, and GPT-J) to identify components responsible for arithmetic. They located key MLPs and attention heads through activation patching, observing that middle- and late-layer MLPs promoted answer prediction. The evaluation showed that only about 1.5% of neurons per layer were needed to achieve high accuracy. These neurons operate as “memorized heuristics,†activating for specific operand patterns and encoding plausible answer tokens.
To solve arithmetic prompts, models use a “bag of heuristics,†where individual neurons recognize specific patterns, and each incrementally contributes to the correct answer’s probability. Neurons are classified by their activation patterns into heuristic types, and neurons within each heuristic are responsible for distinct arithmetic tasks. Ablation tests confirm that each heuristic type causally impacts prompts aligned with its pattern. These heuristic neurons develop gradually throughout training, eventually dominating the model’s arithmetic capability, even as vestigial heuristics emerge mid-training. This suggests that arithmetic proficiency primarily emerges from these coordinated heuristic neurons across training.

LLMs approach arithmetic tasks through heuristic-driven reasoning rather than robust algorithms or memorization. The study reveals that LLMs use a “bag of heuristics,†a mix of learned patterns rather than generalizable algorithms, to solve arithmetic. By identifying specific model components—neurons within a circuit—that handle arithmetic, they found that each neuron activates for specific input patterns, collectively supporting accurate responses. This heuristic-driven method appears early in model training and develops gradually. The findings suggest that enhancing LLMs’ mathematical skills may require fundamental changes in training and architecture beyond current post-hoc techniques.
Check out the Paper. All credit for this research goes to the researchers of this project. Also, don’t forget to follow us on Twitter and join our Telegram Channel and LinkedIn Group. If you like our work, you will love our newsletter.. Don’t Forget to join our 55k+ ML SubReddit.
[Trending] LLMWare Introduces Model Depot: An Extensive Collection of Small Language Models (SLMs) for Intel PCs
The post Decoding Arithmetic Reasoning in LLMs: The Role of Heuristic Circuits over Generalized Algorithms appeared first on MarkTechPost.
Source: Read MoreÂ