Modern machine learning (ML) phenomena such as double descent and benign overfitting have challenged long-standing statistical intuitions, confusing many classically trained statisticians. These phenomena contradict fundamental principles taught in introductory data science courses, especially overfitting and the bias-variance tradeoff. The striking performance of highly overparameterized ML models trained to zero loss contradicts conventional wisdom about model complexity and generalization. This unexpected behavior raises critical questions about the continued relevance of traditional statistical concerns and whether recent developments in ML represent a paradigm shift or reveal previously overlooked approaches to learning from data.
Various researchers have attempted to unravel the complexities of modern ML phenomena. Studies have shown that benign interpolation and double descent are not limited to deep learning but also occur in simpler models like kernel methods and linear regression. Some researchers have revisited the bias-variance tradeoff, noting its absence in deep neural networks and proposing updated decompositions of prediction error. Others have developed taxonomies of interpolating models, distinguishing between benign, tempered, and catastrophic behaviors. These efforts aim to bridge the gap between classical statistical intuitions and modern ML observations, providing a more comprehensive understanding of generalization in complex models.
A researcher from the University of Cambridge has presented a note to understand the discrepancies between classical statistical intuitions and modern ML phenomena such as double descent and benign overfitting. While previous explanations have focused on the complexity of model ML methods, overparameterization, and higher data dimensionality, this study explores a simpler yet often overlooked reason for the observed behaviors. The researchers highlight that statistics historically focused on fixed design settings and in-sample prediction error, whereas modern ML evaluates performance based on generalization error and out-of-sample predictions.
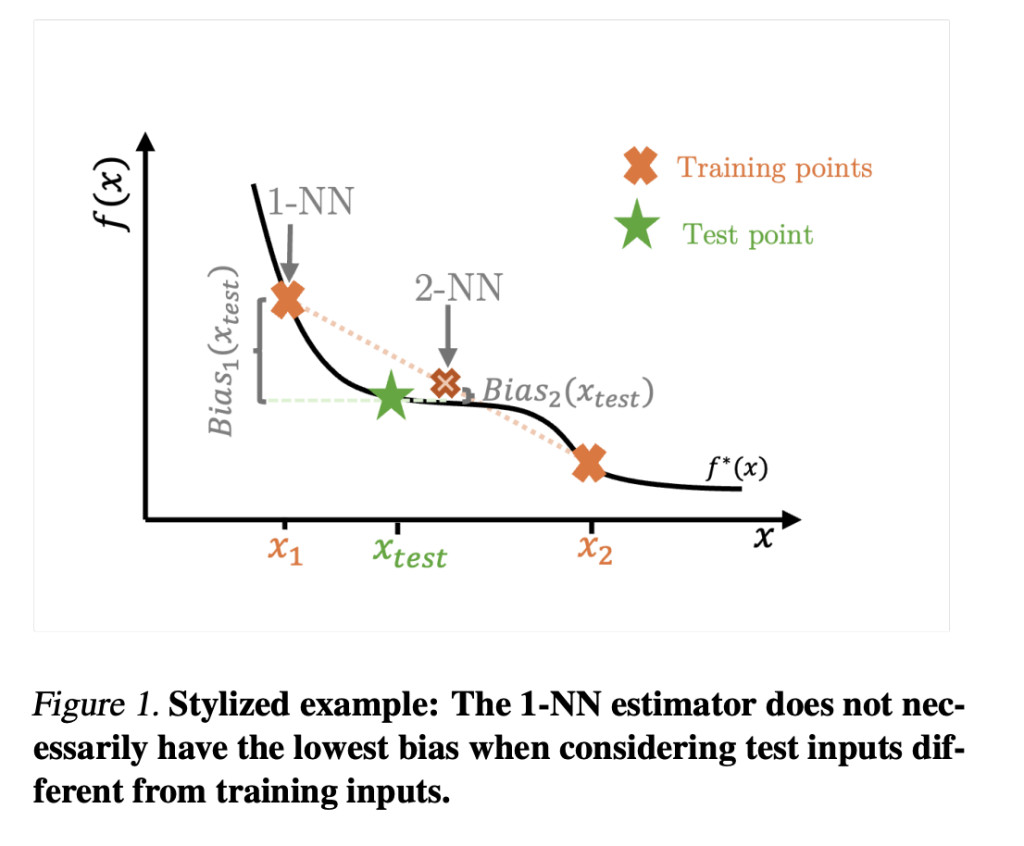
The researchers explore how moving from fixed to random design settings affects the bias-variance tradeoff. The k-nearest Neighbor (k-NN) estimators are used as a simple example to show that surprising behaviors in bias and variance are not limited to complex modern ML methods. Moreover, in the random design setting, the classical intuition that “variance increases with model complexity, while bias decreases†does not necessarily hold. This is because bias no longer monotonically decreases as complexity increases. The key insight is that there is no perfect match between training points and new test points in random design, meaning that even the simplest models may not achieve zero bias. This fundamental difference challenges the traditional understanding of the bias-variance tradeoff and its implications for model selection.
The researchers’ analysis shows that the traditional bias-variance tradeoff intuition breaks down in out-of-sample predictions, even for simple estimators and data-generating processes. While the classical notion that “variance increases with model complexity, and bias decreases†holds for in-sample settings, it doesn’t necessarily apply to out-of-sample predictions. Moreover, there are scenarios where bias and variance decrease as model complexity is reduced, contradicting conventional wisdom. This observation is crucial for understanding phenomena like double descent and benign overfitting. The researchers emphasize that overparameterization and interpolation alone are not responsible for challenging textbook principles.
In conclusion, the researcher from the University of Cambridge highlights a crucial yet often overlooked factor in the emergence of seemingly counterintuitive modern ML phenomena: the shift from evaluating model performance based on in-sample prediction error to generalization to new inputs. This transition from fixed to random designs fundamentally alters the classical bias-variance tradeoff, even for simple k-NN estimators in under-parameterized regimes. This finding challenges the idea that high-dimensional data, complex ML estimators, and over-parameterization are only responsible for these surprising behaviors. This research provides valuable insights into the learning and generalization in contemporary ML landscapes.
Check out the Paper. All credit for this research goes to the researchers of this project. Also, don’t forget to follow us on Twitter and join our Telegram Channel and LinkedIn Group. If you like our work, you will love our newsletter.. Don’t Forget to join our 50k+ ML SubReddit
Interested in promoting your company, product, service, or event to over 1 Million AI developers and researchers? Let’s collaborate!
The post From Fixed to Random Designs: Unveiling the Hidden Factor Behind Modern Machine Learning ML Phenomena appeared first on MarkTechPost.
Source: Read MoreÂ
