Linear programming (LP) solvers are crucial tools in various fields like logistics, finance, and engineering, due to their ability to optimize complex problems involving constraints and objectives. Linear programming (LP) solvers help businesses maximize profits, minimize costs, and improve efficiency by identifying optimal solutions within defined constraints. They are based on the simplex and interior-point methods and struggle with scaling to large problem sizes due to high memory requirements and inefficiency on modern computational hardware like GPUs and distributed systems.
Traditional  Linear programming (LP) solvers rely on matrix factorization techniques such as LU or Cholesky factorization, which are computationally expensive and memory-intensive. As problem sizes grow, these solvers become inefficient, leading to issues like memory overflows and difficulties in utilizing modern computing architectures. First-order methods (FOMs), which update solutions iteratively using gradient information, have gained attention as a scalable alternative to traditional solvers. However, standard FOMs, such as the primal-dual hybrid gradient (PDHG) method, are not yet reliable for LP problems, solving only a small fraction of instances.
Google researchers introduce PDLP (Primal-Dual Hybrid Gradient enhanced for Linear Programming), a new solver built on the restarted PDHG algorithm. PDLP uses matrix-vector multiplication instead of matrix factorization, reducing memory requirements and improving compatibility with modern hardware like GPUs. The tool aims to provide a scalable solution for large-scale LP problems, overcoming the limitations of traditional methods and expanding the applicability of LP to more complex real-world scenarios.
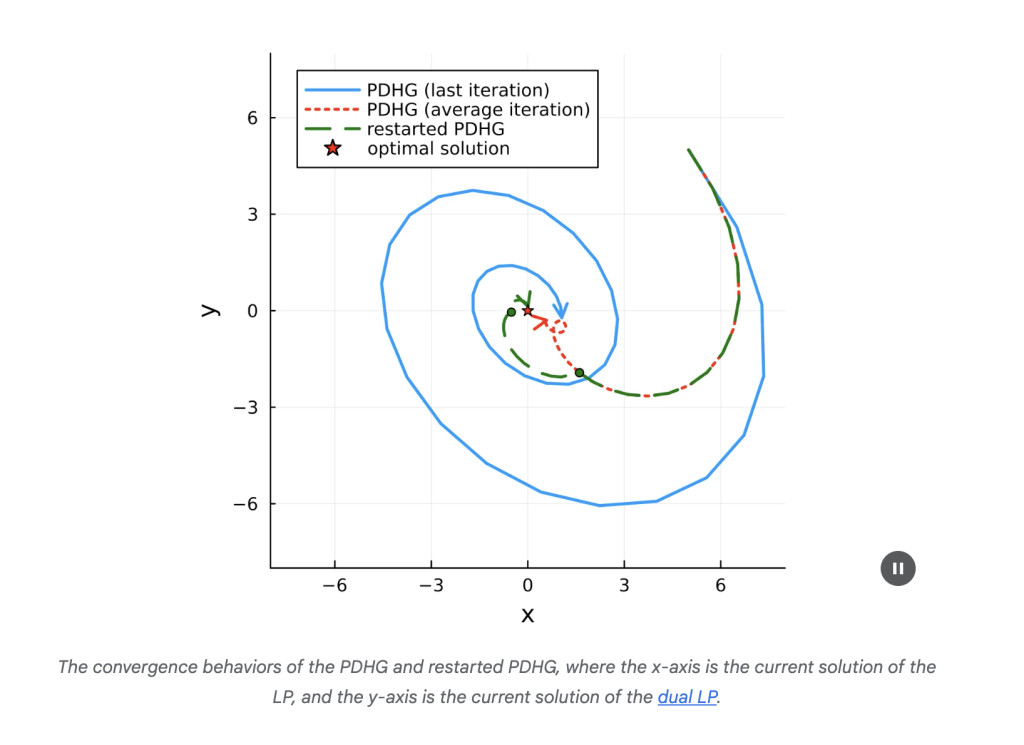
The PDLP (Primal-Dual Hybrid Gradient enhanced for Linear Programming) solver improves the performance and reliability of PDHG by implementing a restarted version of the algorithm. The standard PDHG method, while efficient in handling large-scale computations, is prone to slow convergence. The study introduces a novel technique, the “restarting†mechanism that involves running PDHG until a specific condition is met, averaging the iterations, and then restarting from the average point. This approach shortens the path to convergence by leveraging the cyclic behavior of PDHG, significantly improving the algorithm’s speed.
Additionally, PDLP incorporates several other enhancements, including presolving, preconditioning, infeasibility detection, adaptive restarts, and adaptive step-size selection. These improvements optimize the solver’s performance by simplifying the LP problem, improving numerical conditions, dynamically adjusting algorithmic parameters, and detecting infeasible or unbounded problems early. The performance gains prove that PDLP is highly efficient in both theoretical and practical benchmarks, solving large-scale LP problems that were previously intractable.
In conclusion, the proposed solver successfully addresses the scalability issues in traditional LP solvers. By utilizing an efficient and scalable solver based on the restarted PDHG algorithm, reduces memory requirements, improves performance on modern computational architectures, and solves large-scale LP problems. PDLP’s impact on fields like traffic engineering, container shipping, and the traveling salesman problem demonstrates its practical significance in real-world applications.
Check out the Paper and Blog. All credit for this research goes to the researchers of this project. Also, don’t forget to follow us on Twitter and join our Telegram Channel and LinkedIn Group. If you like our work, you will love our newsletter..
Don’t Forget to join our 50k+ ML SubReddit
The post PDLP (Primal-Dual Hybrid Gradient Enhanced for LP): A New FOM–based Linear Programming LP Solver that Significantly Scales Up Linear Programming LP Solving Capabilities appeared first on MarkTechPost.
Source: Read MoreÂ
