Predicting the long-term behavior of chaotic systems, such as those used in climate modeling, is essential but requires significant computational resources due to the need for high-resolution spatiotemporal grids. One alternative to fully-resolved simulations (FRS) is to use coarse grids, with closure models correcting for errors by approximating the missing fine-scale information. While machine learning methods have recently been applied to improve closure models, they still face obstacles, including the need for large amounts of costly high-resolution training data and, at times, requiring coarse-grid simulations derived from downsampled FRS data.
Researchers from Caltech have discovered a key limitation in traditional closure models for predicting long-term statistics of chaotic systems. These models suffer from high approximation errors due to non-unique mappings. To address this, they developed a physics-informed neural operator (PINO) that eliminates the need for closure models and coarse-grid solvers. PINO is first trained on coarse-grid data and then fine-tuned with a small amount of high-fidelity simulation data and physics-based constraints. This grid-free approach allows PINO to accurately estimate long-term statistics with a 120× speedup and only ~5% error, outperforming conventional, slower, and much less accurate closure models. Theoretical and experimental results in fluid dynamics validate PINO’s effectiveness.
The problem involves evaluating long-term statistics of dynamical systems governed by partial differential equations (PDEs). High-fidelity simulations (FRS) offer accurate solutions but are computationally expensive, especially for chaotic systems requiring dense spatiotemporal grids. Coarse-grid simulations (CGS) aim to reduce this cost by estimating statistics using closure models. Traditional closure models rely on simplifying assumptions, while machine learning-based methods offer alternatives but face challenges like non-uniqueness and dependence on extensive training data from FRS. These methods often require significant amounts of fine-grid data and can be computationally prohibitive, limiting their broader application.
The researchers introduce a physics-informed operator learning method to address the limitations of traditional closure models in predicting long-term statistics of chaotic systems. Instead of learning on a coarse grid, they extend the task to the entire function space by directly modeling the solution operator of the governing PDE. Using Fourier Neural Operators (FNO), their approach is resolution-invariant and achieves faster convergence by taking larger time steps. They incorporate physics-informed loss functions and pre-train the model with coarse-grid data before fine-tuning with limited high-fidelity simulations. Theoretical results demonstrate that their method accurately estimates long-term statistics, ensuring robust performance even with approximate operators.
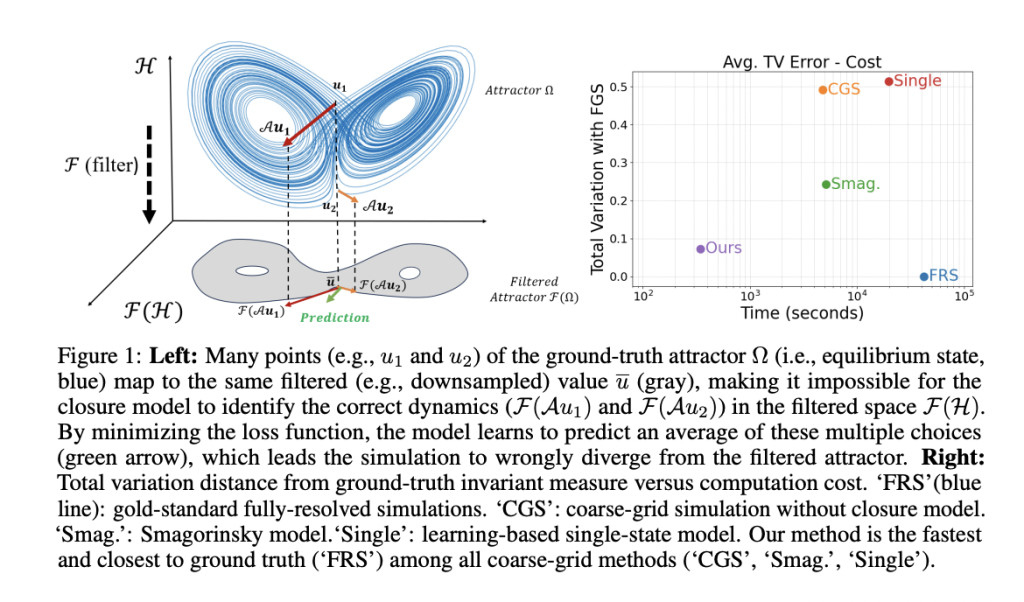
The study validates their physics-informed operator learning method on two fluid dynamics equations: the 1D Kuramoto-Sivashinsky (KS) and 2D Navier-Stokes (NS). Using Fourier Neural Operators (FNO) and minimal FRS data, their model outperforms traditional CGS and closure models in estimating long-term statistics. Comparisons of the energy spectrum, vorticity, and velocity variance show significantly lower errors than baselines, such as the Smagorinsky model and single-state learning-based methods. Despite limited FRS data, their approach yields accurate predictions efficiently, with superior performance in realistic settings compared to previous learning-based methods.
The study addresses the challenge of estimating long-term statistics in chaotic systems using coarse-grid simulations. The researchers propose a functional Liouville flow framework and demonstrate the limitations of traditional learning methods. Using PINO, they achieve efficient, accurate predictions with minimal fine-resolution data. PINO bypasses coarse-grid solvers, unlike closure models, offering a more robust solution. Experiments show significant improvements, achieving a 120x speedup with only ∼5% error, compared to the slower and less accurate closure models. This approach has broad applications, including climate modeling and image generation tasks.
Check out the Paper. All credit for this research goes to the researchers of this project. Also, don’t forget to follow us on Twitter and join our Telegram Channel and LinkedIn Group. If you like our work, you will love our newsletter..
Don’t Forget to join our 50k+ ML SubReddit
The post Efficient Long-Term Prediction of Chaotic Systems Using Physics-Informed Neural Operators: Overcoming Limitations of Traditional Closure Models appeared first on MarkTechPost.
Source: Read MoreÂ
