Deep generative models learn continuous data representations from a limited set of training samples, with global metrics like Fréchet Inception Distance (FID) often used to evaluate their performance. However, these models may perform inconsistently across different regions of the learned manifold, especially in foundation models like Stable Diffusion, where generation quality can vary based on conditioning or initial noise. The rise in generative model capabilities has driven the need for more detailed evaluation methods, including metrics that assess fidelity and diversity separately and human evaluations that address concerns like bias and memorization.
Researchers from Google, Rice University, McGill University, and Google DeepMind explore the connection between the local geometry of generative model manifolds and the quality of generated samples. They use three geometric descriptors—local scaling, rank, and complexity—to analyze the manifold of a pre-trained model. Their findings reveal correlations between these descriptors and factors like generation aesthetics, artifacts, uncertainty, and memorization. Additionally, they demonstrate that training a reward model on these geometric properties can influence the likelihood of generated samples, enhancing control over the diversity and fidelity of outputs, particularly in models like Stable Diffusion.
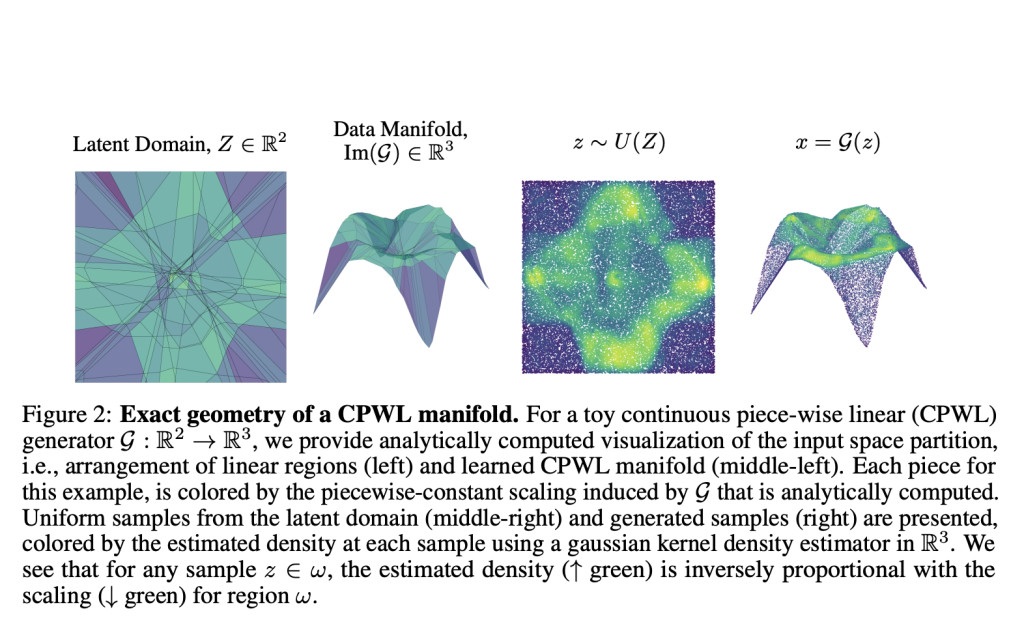
The researchers discuss continuous piecewise-linear (CPWL) generative models, which include decoders of VAEs, GAN generators, and DDIMs. These models map input space to output space through affine operations, resulting in a partitioned input space with each region mapped to the data manifold. They define local geometric descriptors—complexity, scaling, and rank—to analyze the learned manifold’s smoothness, density, and dimensionality. A toy example illustrates that higher local scaling correlates with lower sample density, and local complexity varies across regions. These descriptors help guide the generation process by influencing sample characteristics based on manifold geometry.
The study explores the geometry of data manifolds learned by various generative models, focusing on denoising diffusion probabilistic models (DDPMs) and Stable Diffusion. It examines the relationship between local geometric descriptors (complexity, scaling, and rank) and factors like noise levels, model training steps, and prompt guidance. The study reveals that higher noise or guidance scales typically increase model complexity and quality, while memorized prompts result in lower uncertainty. The analysis of ImageNet and out-of-distribution samples, such as X-rays, demonstrates that local geometry can effectively distinguish between in- and out-of-domain data, impacting generation diversity and quality.
The study explores how geometric descriptors, particularly local scaling, can guide generative models to produce varied and detailed outputs. The generative process can be steered using classifier guidance to maximize local scaling, leading to sharper, more textured images with higher diversity. Conversely, they minimize local scaling, resulting in blurred photos with reduced detail. A reward model approximates local scaling, enabling instance-level intervention in the generative process. This approach enhances diversity at the image level, offering a precise method for controlling the output of generative models.
The study introduces a self-assessment method for generative models using geometry-based descriptors—local scaling, rank, and complexity—without relying on training data or human evaluators. These descriptors help evaluate the learned manifold’s uncertainty, dimensionality, and smoothness, revealing insights into generation quality, diversity, and biases. The study highlights the impact of manifold geometry on model performance. Still, it acknowledges two key limitations: the influence of training dynamics on manifold geometry and the computational challenges, especially with large models. Future research should focus on understanding this relationship and developing more efficient computational methods.
Check out the Paper. All credit for this research goes to the researchers of this project. Also, don’t forget to follow us on Twitter and join our Telegram Channel and LinkedIn Group. If you like our work, you will love our newsletter..
Don’t Forget to join our 48k+ ML SubReddit
Find Upcoming AI Webinars here
The post Geometry-Guided Self-Assessment of Generative AI Models: Enhancing Diversity, Fidelity, and Control appeared first on MarkTechPost.
Source: Read MoreÂ