Gradient descent-trained neural networks operate effectively even in overparameterized settings with random weight initialization, often finding global optimum solutions despite the non-convex nature of the problem. These solutions, achieving zero training error, surprisingly do not overfit in many cases, a phenomenon known as “benign overfitting.†However, for ReLU networks, interpolating solutions can lead to overfitting. Moreover, the best solutions usually don’t interpolate the data in noisy data scenarios. Practical training often stops before reaching full interpolation to avoid entering unstable regions or spiky, non-robust solutions.
Researchers from UC Santa Barbara, Technion, and UC San Diego explore the generalization of two-layer ReLU neural networks in 1D nonparametric regression with noisy labels. They present a new theory showing that gradient descent with a fixed learning rate converges to local minima representing smooth, sparsely linear functions. These solutions, which do not interpolate, avoid overfitting and achieve near-optimal mean squared error (MSE) rates. Their analysis highlights that large learning rates induce implicit sparsity and that ReLU networks can generalize well even without explicit regularization or early stopping. This theory moves beyond traditional kernel and interpolation frameworks.
In overparameterized neural networks, most research focuses on generalization within the interpolation regime and benign overfitting. These typically require explicit regularization or early stopping to handle noisy labels. However, recent findings indicate that gradient descent with a large learning rate can achieve sparse, smooth functions that generalize well, even without explicit regularization. This method diverges from traditional theories, which rely on interpolation, demonstrating that gradient descent induces an implicit bias resembling L1-regularization. The study also connects to the hypothesis that “flat local minima generalize better†and provides insights into achieving optimal rates in nonparametric regression without weight decay.
The study addresses the setup and notation for studying generalization in two-layer ReLU neural networks. The model is trained using gradient descent on a dataset with noisy labels, focusing on regression problems. Key concepts include stable local minima, which are twice differentiable and lie within a specific distance from the global minimum. The study also explores the “Edge of Stability†regime, where the Hessian’s largest eigenvalue reaches a critical value related to the learning rate. For nonparametric regression, the target function is from a bounded variation class. The analysis demonstrates that gradient descent cannot find stable interpolating solutions in noisy settings, leading to smoother, non-interpolating functions.
The study’s main results explore stable solutions for gradient descent (GD) on ReLU neural networks across three aspects. First, it examines the implicit bias of stable solutions in the function space under large learning rates, revealing that they are inherently smoother and simpler. Second, it derives generalization bounds for these solutions in distribution-free and non-parametric regression settings, showing they avoid overfitting. Lastly, the analysis demonstrates that GD achieves optimal rates for estimating bounded variation functions within specific intervals, confirming the effective generalization performance of large learning rate GD solutions even in noisy environments.
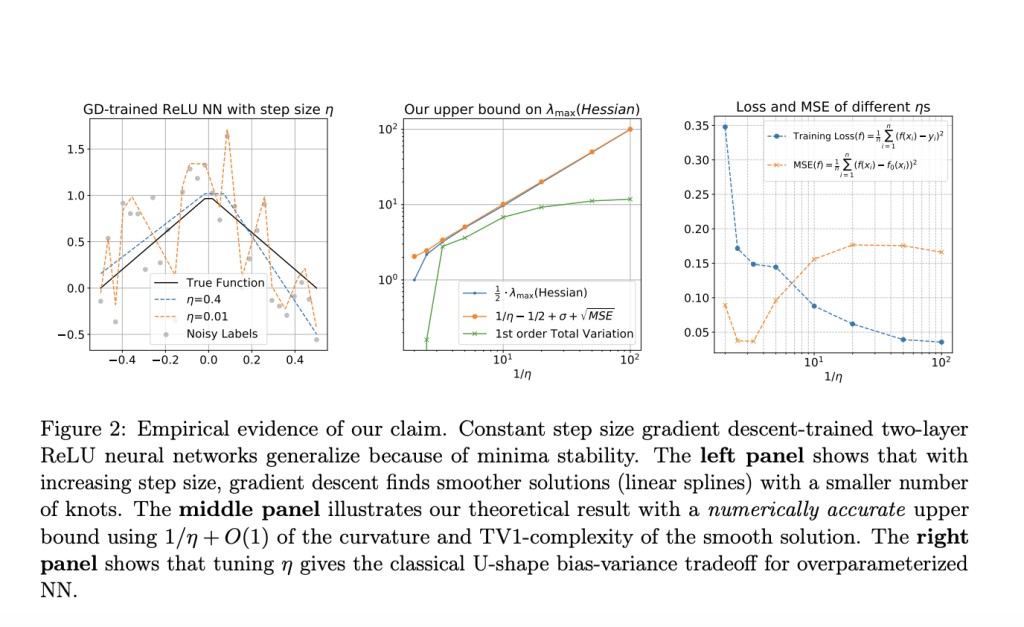
In conclusion, the study explores how gradient descent-trained two-layer ReLU neural networks generalize through the lens of minima stability and the Edge-of-Stability phenomena. It focuses on univariate inputs with noisy labels and shows that gradient descent with a typical learning rate cannot interpolate data. The study demonstrates that local smoothness of the training loss implies a first-order total variation constraint on the neural network’s function, leading to a vanishing generalization gap within the data support’s strict interior. Additionally, these stable solutions achieve near-optimal rates for estimating first-order bounded variation functions under a mild assumption. The simulations validate the findings, showing that large learning rate training induces sparse linear spline fits.
Check out the Paper. All credit for this research goes to the researchers of this project. Also, don’t forget to follow us on Twitter.Â
Join our Telegram Channel and LinkedIn Group.
If you like our work, you will love our newsletter..
Don’t Forget to join our 44k+ ML SubReddit
The post Generalization of Gradient Descent in Over-Parameterized ReLU Networks: Insights from Minima Stability and Large Learning Rates appeared first on MarkTechPost.
Source: Read MoreÂ