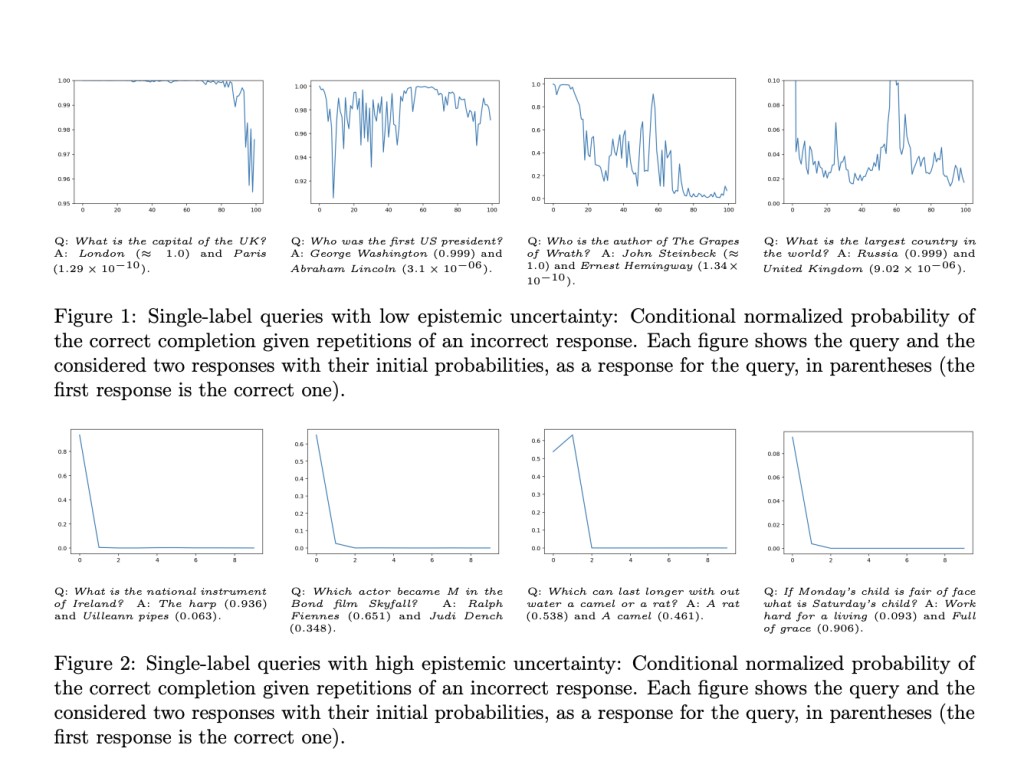
This paper explores the domain of uncertainty quantification within large language models (LLMs) to identify scenarios where uncertainty in response to queries is significant. The study encompasses both epistemic and aleatoric uncertainties. Epistemic uncertainty arises from a lack of knowledge or data about the ground truth, whereas aleatoric uncertainty stems from inherent randomness in the prediction problem. Properly identifying these uncertainties is crucial for enhancing the reliability and truthfulness of LLM responses, especially to detect and mitigate hallucinations or inaccurate responses generated by these models.
There are currently several methods for detecting hallucinations in large language models (LLMs), each with its own set of limitations. One common method is the probability of the greedy response (T0), which assesses the likelihood of the most probable response generated by the model. Another method is the semantic-entropy method (S.E.), which measures the entropy of the semantic distribution of the responses. Finally, the self-verification method (S.V.) involves the model verifying its responses to estimate uncertainty.
Despite their usefulness, these methods have notable drawbacks. The probability of the greedy response is often sensitive to the size of the label set, meaning it may not perform well when there are many possible responses. The semantic-entropy method (S.E.) relies on first-order scores that do not consider the joint distribution of responses, which can lead to incomplete uncertainty assessments. Similarly, the self-verification method (S.V.) does not account for the full range of possible responses the model can generate, potentially overlooking significant aspects of uncertainty.
To overcome the limitations of current methods, the proposed approach involves creating a combined distribution for multiple responses from the LLM for a specific query using iterative prompting. This involves asking the LLM to generate a response to a query and then asking it to generate subsequent responses while including previous ones in the prompt. The joint distribution approximates the ground truth if the responses are independent, indicating low epistemic uncertainty. However, if the responses are influenced by each other, it signifies high epistemic uncertainty. This iterative prompting procedure allows the researchers to derive an information-theoretic metric of epistemic uncertainty. They quantify this by measuring the mutual information (MI) of the joint distribution of responses, which is insensitive to aleatoric uncertainty. A finite-sample estimator for this MI is developed, proving to have negligible error in practical applications despite the potentially infinite support of LLM outputs.
An algorithm for hallucination detection based on this MI metric is also discussed. By setting a threshold through a calibration procedure, the method demonstrates superior performance compared to traditional entropy-based approaches, especially in datasets with mixed single-label and multi-label queries. It maintains high recall rates while minimizing errors, making it a robust tool for improving the reliability of LLM outputs.
This paper presents a significant advancement in quantifying uncertainty in LLMs by distinguishing between epistemic and aleatoric uncertainty. The proposed iterative prompting and mutual information-based metric offer a more nuanced understanding of LLM confidence, enhancing the detection of hallucinations and improving overall response accuracy. This approach addresses a critical limitation of existing methods and provides a practical and effective solution for real-world applications of LLMs.Â
Check out the Paper. All credit for this research goes to the researchers of this project. Also, don’t forget to follow us on Twitter. Join our Telegram Channel, Discord Channel, and LinkedIn Group.
If you like our work, you will love our newsletter..
Don’t Forget to join our 44k+ ML SubReddit
The post Deciphering Doubt: Navigating Uncertainty in LLM Responses appeared first on MarkTechPost.
Source: Read MoreÂ