Search
News & Updates
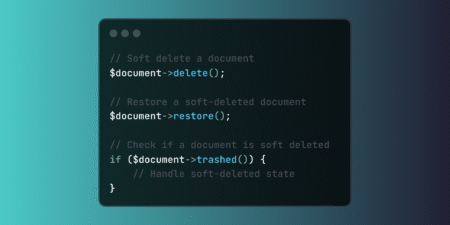
Implement Laravel soft deletes to preserve data integrity while enabling logical deletion. This powerful feature supports compliance requirements, audit trails, and data recovery scenarios without permanent data loss. The post Preserving Data Integrity with Laravel Soft Deletes for Recovery and Compliance appeared first on Laravel News. Join the Laravel Newsletter…
We are excited to share that Pest 4 is now available! Get started with browser testing in Pest using modern tools, visual testing, and more! The post Pest 4 is Released appeared first on Laravel News. Join the Laravel Newsletter to get all the latest Laravel articles like this directly…
Useful Laravel links to read/watch for this week of August 21, 2025. Source: Read MoreÂ
A Laravel package for generating Bootstrap 5 forms based on models. The post Quickly Generate Forms based on your Eloquent Models with Laravel Formello appeared first on Laravel News. Join the Laravel Newsletter to get all the latest Laravel articles like this directly in your inbox. Source: Read MoreÂ
Artificial Intelligence
Training Diffusion Models with Reinforcement Learning We deployed 100 reinforcement learning (RL)-controlled cars into rush-hour…
PLAID is a multimodal generative model that simultaneously generates protein 1D sequence and 3D structure,…
Recent advances in Large Language Models (LLMs) enable exciting LLM-integrated applications. However, as LLMs have…
In order to produce effective targeted therapies for cancer, scientists need to isolate the genetic…