Accurately modeling magnetic hysteresis is a significant challenge in the field of AI, especially for optimizing the performance of magnetic devices such as electric machines and actuators. Traditional methods often struggle to generalize to novel magnetic fields, limiting their effectiveness in real-world applications. Addressing this challenge is crucial for developing efficient and generalizable models that can predict hysteresis behavior under varying conditions.
Current methods for modeling magnetic hysteresis include traditional neural networks like recurrent neural networks (RNNs), long short-term memory (LSTM) networks, and gated recurrent units (GRUs). These methods leverage the universal function approximation property to model the hysteresis relationship between applied magnetic fields (H) and magnetic flux density (B). However, they primarily achieve accuracy only for specific excitations used during training, failing to generalize to novel magnetic fields. This limitation arises from their inability to model mappings between functions in continuous domains, which is crucial for accurately predicting hysteresis behavior under varying conditions.
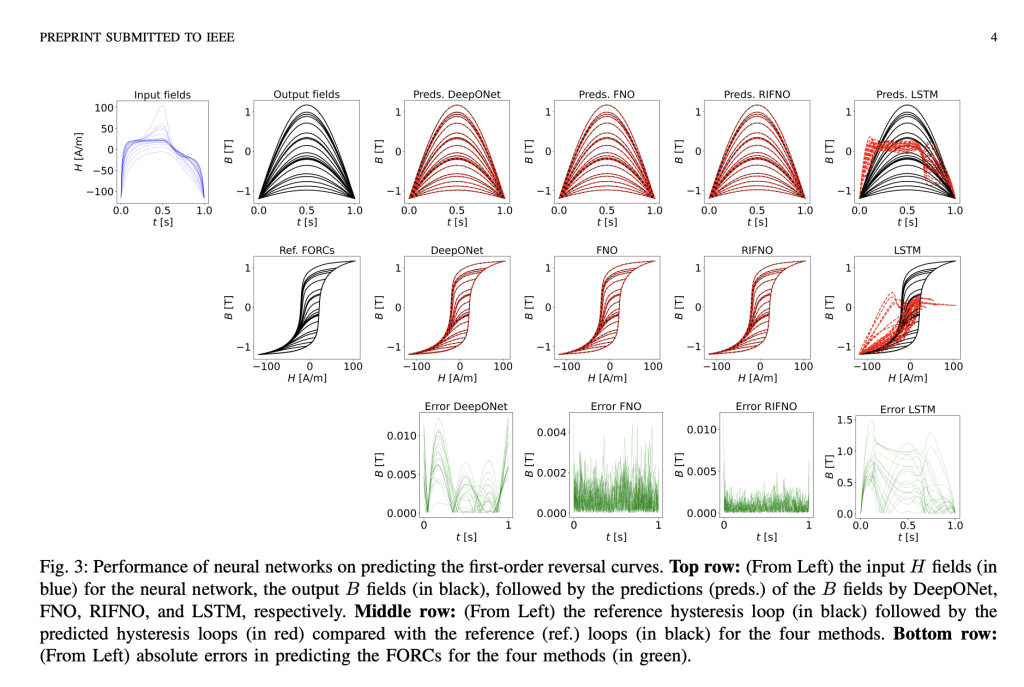
The researchers propose using neural operators, specifically the Deep Operator Network (DeepONet) and Fourier Neural Operator (FNO), to model the hysteresis relationship between magnetic fields. Neural operators differ from traditional neural networks by approximating the underlying operator that maps H fields to B fields, allowing for generalization to novel magnetic fields. Additionally, a rate-independent Fourier Neural Operator (RIFNO) is introduced to predict material responses at different sampling rates, addressing the rate-independent characteristic of magnetic hysteresis. This approach represents a significant contribution by offering a more efficient and accurate solution compared to existing methods.
The proposed method involves training neural operators on datasets generated using a Preisach-based model of the material NO27-1450H. The datasets include first-order reversal curves (FORCs) and minor loops, with inputs normalized using min-max scaling. The DeepONet architecture comprises two fully connected feedforward neural networks (branch and trunk nets) that approximate the B fields through a dot product operation. The FNO uses a convolutional neural network architecture with Fourier layers to transform the input tensor and approximate the B fields. The RIFNO modifies the FNO architecture to exclude the sampling array, making it invariant to sampling rates and suitable for modeling rate-independent hysteresis.
The proposed method’s performance was evaluated using three error metrics: relative error in L2 norm, mean absolute error (MAE), and root mean squared error (RMSE). The neural operators, particularly FNO and RIFNO, showed superior accuracy and generalization capability compared to traditional recurrent architectures. The FNO exhibited the lowest errors, with a relative error of 1.34e-3, MAE of 7.48e-4, and RMSE of 9.74e-4, highlighting its effectiveness in modeling magnetic hysteresis. The RIFNO also maintained low prediction errors across various testing rates, demonstrating robustness and the ability to generalize well under different conditions. In contrast, traditional recurrent models like RNN, LSTM, and GRU showed significantly higher errors and struggled to predict responses for novel magnetic fields.
In conclusion, the researchers introduced a novel approach to magnetic hysteresis modeling using neural operators, addressing the limitations of traditional neural networks in generalizing to novel magnetic fields. The proposed methods, DeepONet and FNO, along with the rate-independent RIFNO, demonstrate superior accuracy and generalization capability. This research advances the field of AI by developing efficient and accurate models for magnetic materials, enabling real-time inference and broadening the applicability of neural hysteresis modeling.
Check out the Paper. All credit for this research goes to the researchers of this project. Also, don’t forget to follow us on Twitter and join our 46k+ ML SubReddit, 26k+ AI Newsletter, Telegram Channel, and LinkedIn Group.
If You are interested in a promotional partnership (content/ad/newsletter), please fill out this form.
The post This Paper Addresses the Generalization Challenge by Proposing Neural Operators for Modeling Constitutive Laws appeared first on MarkTechPost.
Source: Read MoreÂ