Machine learning, particularly DNNs, plays a pivotal role in modern technology, influencing innovations like AlphaGo and ChatGPT and integrating them into consumer products such as smartphones and autonomous vehicles. Despite their widespread applications in computer vision and natural language processing, DNNs are often criticized for their opacity. They remain challenging to interpret due to their intricate, nonlinear nature and the variability introduced by factors like data noise and model configuration. Efforts towards interpretability include architectures employing attention mechanisms and feature interpretability, yet understanding and optimizing DNN training processes, which involve complex interactions between model parameters and data, remain central challenges.
Researchers from the Network Science and Technology Center and Department of Computer Science at Rensselaer Polytechnic Institute and collaborators from IBM Watson Research Center and the University of California have developed a mathematical framework. This framework maps neural network performance to the characteristics of a line graph governed by stochastic gradient descent’s edge dynamics through differential equations. It introduces a neural capacitance metric to universally assess a model’s generalization capability early in training, enhancing model selection efficiency across diverse benchmarks and datasets. This approach employs network reduction techniques to handle the computational complexity of millions of weights in neural networks like MobileNet and VGG16, significantly advancing AI problems such as learning curve prediction and model selection.
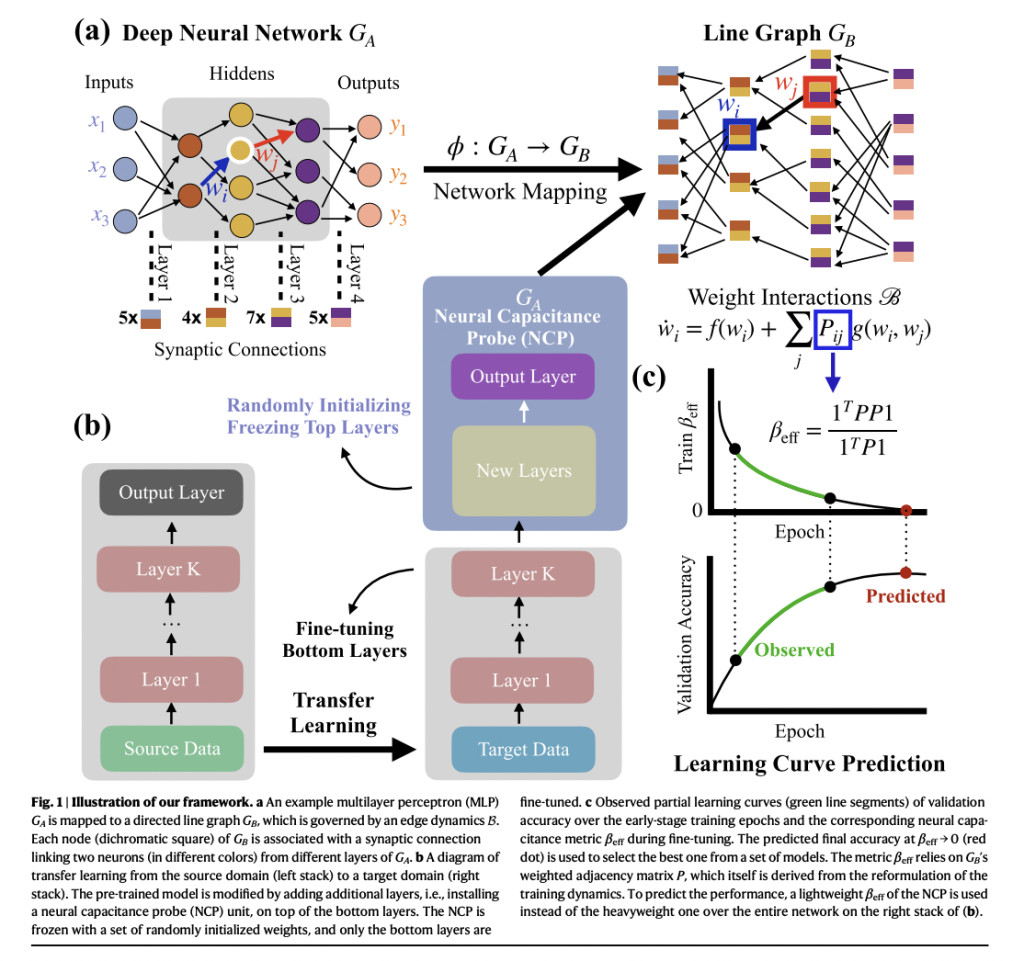
The authors explore methods for analyzing networked systems, such as ecological or epidemic networks, modeled as graphs with nodes and edges. These networks are described by differential equations that capture interactions between nodes, influenced by both internal dynamics and external factors. The network’s adjacency matrix plays a crucial role in encoding the strength of interactions between nodes. To manage the complexity of large-scale systems, a mean-field approach is employed, using a linear operator derived from the adjacency matrix to decouple and analyze the network dynamics effectively.
In neural networks, training involves nonlinear optimization through forward and backward propagation. This process is akin to dynamical systems, where nodes (neurons) and edges (synaptic connections) evolve based on gradients derived from the training error. The interactions between weights in neural networks are quantified using a metric called neural capacitance, analogous to network resilience metrics in other complex systems. Bayesian ridge regression is applied to estimate this neural capacitance, providing insights into how network properties influence predictive accuracy. This framework helps in understanding and predicting the behavior of neural networks during training, drawing parallels with methods used in analyzing real-world networked systems.
The study introduces a method to analyze neural networks by mapping them onto graph structures, facilitating detailed analysis using network science principles. Neural network layers are represented as nodes in a graph, with edges corresponding to synaptic connections, treated dynamically based on training dynamics. A key metric, βeff, derived from these dynamics, predicts model performance early in training. This approach demonstrates robustness across various pretrained models and datasets, outperforming traditional predictors like learning curve-based and transferability measures. The method’s efficiency is highlighted, requiring minimal computational resources compared to full training, thus offering insights into neural network behavior and enhancing model selection processes.
Understanding network function from structure is crucial across diverse applications in Network Science. This study delves into neural network dynamics during training, exploring complex interactions and emergent behaviors like sparse sub-networks and gradient descent convergence patterns. The approach maps neural networks to graphs, capturing synaptic connection dynamics through an edge-based model. A key metric, βeff, derived from this model, effectively predicts model performance early in training. Future directions include refining synaptic interaction modeling, expanding to neural architecture search benchmarks, and developing direct optimization algorithms for neural network architectures. This framework enhances insights into neural network behavior and improves model selection processes.
Check out the Paper. All credit for this research goes to the researchers of this project. Also, don’t forget to follow us on Twitter.Â
Join our Telegram Channel and LinkedIn Group.
If you like our work, you will love our newsletter..
Don’t Forget to join our 46k+ ML SubReddit
The post Mapping Neural Networks to Graph Structures: Enhancing Model Selection and Interpretability through Network Science appeared first on MarkTechPost.
Source: Read MoreÂ