Enhancing Mathematical Reasoning in LLMs: Integrating Monte Carlo Tree Search with Self-Refinement

With the rapid advancements in artificial intelligence, LLMs such as GPT-4 and LLaMA have significantly enhanced natural language processing. These models, boasting billions of parameters, excel in understanding and generating language, enabling new capabilities in complex tasks like mathematical problem-solving, recommendation systems, and molecule generation. Despite their strengths, LLMs struggle with tasks requiring precise reasoning, often producing errors or “hallucinations,” especially in mathematical contexts. Although methods like Self-Refine can mitigate this issue, these inaccuracies can still lead to misleading or incorrect results in complex real-world applications.

Researchers from Fudan University and the Shanghai Artificial Intelligence Laboratory have developed the MCT Self-Refine (MCTSr) algorithm, combining LLMs with Monte Carlo Tree Search (MCTS) to enhance mathematical reasoning. This integration leverages MCTS’s systematic exploration and LLMs’ self-refinement capabilities to improve decision-making in complex tasks. MCTSr addresses the stochastic nature of LLM outputs with a dynamic pruning strategy and an improved Upper Confidence Bound (UCB) formula. The algorithm significantly boosts success rates in solving Olympiad-level math problems, showcasing its potential to advance AI-driven decision-making and problem-solving. 

MCTS has been effectively applied across diverse domains to tackle complex problems, from optimizing multi-agent pathfinding to solving the Train Timetabling Problem (TTP) and various SAT problems. Recent innovations include integrating MCTS with physics-informed neural networks for dynamic robotics tasks. In parallel, advancements in LLMs have enhanced their mathematical reasoning, yet they still need help with multi-step reasoning errors. Researchers are exploring combining MCTS with LLMs to improve decision-making and refine responses, leveraging MCTS’s strategic exploration and LLMs’ self-refinement and evaluation capabilities for better performance on complex reasoning tasks.

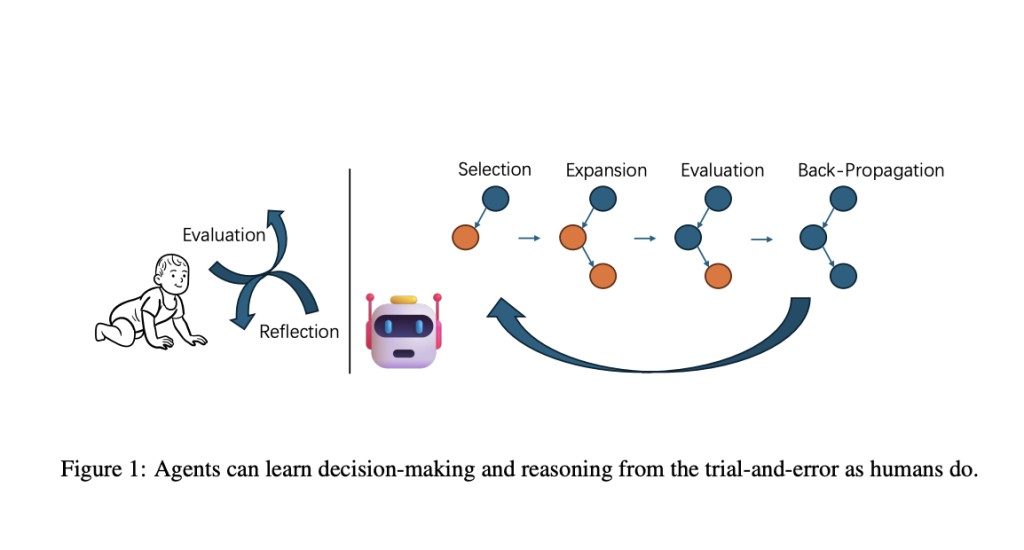
MCTS is a decision-making algorithm that explores vast problem spaces, typically in games and complex tasks. It involves four stages: Selection, where promising nodes are chosen based on potential; Expansion, adding new nodes to the tree; Simulation, running random outcomes to estimate node values; and Backpropagation, updating parent nodes with simulation results. The MCTSr algorithm integrates MCTS with large language models to enhance answer quality in complex reasoning tasks. It iteratively refines answers through self-improvement and evaluates them with self-rewarding mechanisms, balancing exploration and exploitation to optimize decision-making.

To evaluate the MCTSr algorithm’s effectiveness, the LLaMA3-8B model was enhanced with MCTSr and tested on various mathematical benchmarks. These benchmarks included GSM8K, GSM-Hard, MATH, AIME, Math Odyssey, and OlympiadBench. Results indicated a clear correlation between increased MCTSr rollouts and higher success rates, particularly in simpler problems. However, performance plateaued on more complex datasets, showing the limitations of the current approach. Comparisons with top closed-source models like GPT-4 and Claude 3 demonstrated that MCTSr significantly boosts the mathematical problem-solving capabilities of open-source models, suggesting its potential to enhance academic problem-solving tools.

The MCTSr algorithm has shown significant promise in enhancing the ability of LLMs to tackle complex mathematical problems. By combining MCTS with LLMs, MCTSr significantly improves accuracy and reliability in mathematical reasoning tasks. Experimental evaluations across various datasets, including challenging Olympiad-level problems, highlight substantial improvements in problem-solving success rates. While the current focus is on mathematical applications, the broader potential of MCTSr in areas such as black-box optimization and self-driven alignment for LLMs suggests promising avenues for future research. Further exploration and optimization are needed to realize its versatility and effectiveness fully.

Check out the Paper. All credit for this research goes to the researchers of this project. Also, don’t forget to follow us on Twitter. 

Join our Telegram Channel and LinkedIn Group.

If you like our work, you will love our newsletter..

Don’t Forget to join our 44k+ ML SubReddit

The post Enhancing Mathematical Reasoning in LLMs: Integrating Monte Carlo Tree Search with Self-Refinement appeared first on MarkTechPost.

Source: Read More